Beta barium borate
Beta barium borate (β-barium borate, BBO or β-BaB2O4) is a crystal frequently used for frequency mixing and other nonlinear optics applications. It has a wide transmission range, from approximately 200 nanometres to beyond 3 micrometres, and is used particularly for its transparency in the deep ultraviolet.
BBO has a trigonal crystal system, belongs to crystallographic point group 3m, and belongs to the crystallographic space group R3c. BBO has strong negative uniaxial birefringence and can be phase-matched for type I (ooe) second harmonic generation from 409.6 to 3500 nm. The temperature sensitivity of the indices of refraction is low, leading to an unusually large (55 °C) temperature phase-matching bandwidth. The crystal is mildly hygroscopic.
β-Barium borate differs from α-barium borate in the positions of the barium ions within the crystal. Both phases are birefringent, however the α phase, which exists above 925 °C, possesses centric symmetry and thus does not have the same nonlinear properties as the β phase.[1]
The nonlinear nature of BBO allows for the production of pairs of photons via spontaneous parametric down-conversion. This is an important resource for experimental quantum information, particularly as a method of producing entangled photons.[2]
Contents |
Physical properties
- Lattice parameters: a=b=1.253 nm, c=1.272 nm, Z=6
- Melting point: 1095±5 °C
- Phase transition temperature: 925±5 °C
- Mohs hardness: 4.5
- Density: 3.85 g/cm3
Optical properties
- Refractive index, 1064 nm:
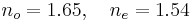
- Refractive index, 532 nm:
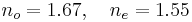
- Refractive index, 266 nm:
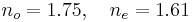
- Transparency range (> 0.5 cm−1): 198–2600 nm[1]
- Thermo-optic coefficients:[1]
- Nonlinear optical coefficients:[3]
- d22 = 2.3 pm/V
- d31 = -0.16 pm/V
- High damage threshold of 10 GW/cm2 for 100 ps pulse-width at 1064 nm.
Sellmeier equations (for λ in micrometres)
References
- ^ a b c D. N. Nikogosyan. "Beta Barium Borate (BBO)". Applied Physics A 52: 359–368.
- ^ Gerry, C; Knight, P (2005). Introductory quantum mechanics. Campbridge University Press. ISBN 9780521527354. http://books.google.com/?id=CgByyoBJJwgC&printsec=frontcover&dq=gerry+and+Knight#v=onepage&q&f=false., [1]
- ^ V.G. Dmitriev, G. G. Gurzadyan, and D. N. Nikogosyan (1999). Handbook of Nonlinear Optical Crystals, 3rd edition. Springer. ISBN 0342-4111.
- ^ a b Kato, K. (1986). "Second-harmonic generation to 2048 Å in β-BaB2O4". IEEE Journal of Quantum Electronics 22 (7): 1013–1014. Bibcode 1986IJQE...22.1013K. doi:10.1109/JQE.1986.1073097.
External links
- "BBO Crystal β-Barium Borate". Photox Optical Systems website. http://www.photox.co.uk/bbo.htm. Retrieved 2006-10-23.
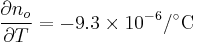
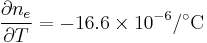
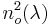 = 2.7359+0.01878/(λ2 - 0.01822)-0.01354 λ2
= 2.7359+0.01878/(λ2 - 0.01822)-0.01354 λ2 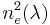 = 2.3753+0.01224/(λ2-0.01667)-0.01516 λ2
= 2.3753+0.01224/(λ2-0.01667)-0.01516 λ2